Animoog Complex Timbre
Complex Single Cycle Waveforms composed of multiple single cycle waves.
The AKWF_birds_0002 example in the timbre tutorial shows there can be significant issues to take into consideration with complex single cycle wave forms with respect to tuning. There are in fact 9 slightly different wave forms in the AKWF_birds_0002 sample as shown in the screen shot.
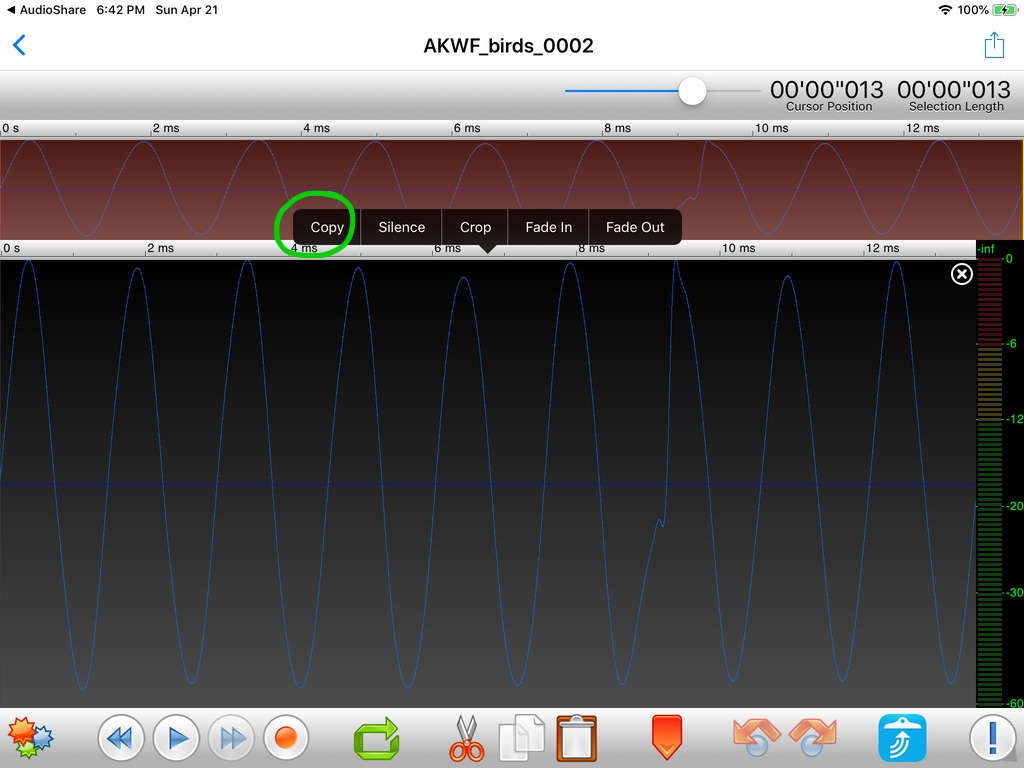
Rather than being a frequency of 1/0.013 Hz = 76.9 Hz, the sample’s true frequency will be 9/0.013 Hz = 692.3 Hz which is the difference between D#2 minus 20 cents versus F5 minus 15 cents. The frequency we want will be 16/0.371 Hz = 2.70 Hz for the Animoog timbre.
The question then becomes how do you fit a single cycle waveform composed of 9 different waves into a 16 single cycle Animoog timbre? Perhaps 18 cycles of the sample into the time 18 Animoog single cycle forms would have fit which would be 1024x18 = 18432 samples or 0.418 seconds versus the normal 1024x16 = 16384 samples or 0.371 seconds?
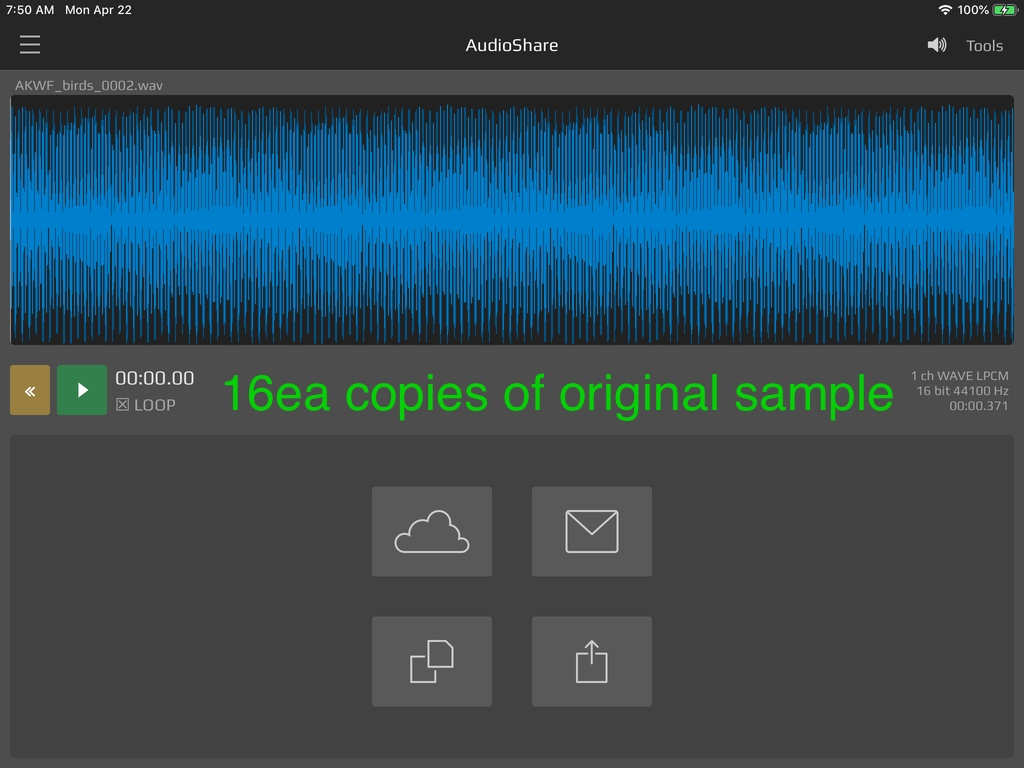
You could choose to trim your sample down to 8 single cycle waves from the original 9 single cycles so that you can pitch/time stretch to end up with 16 single cycle wave forms for your timbre as shown below.
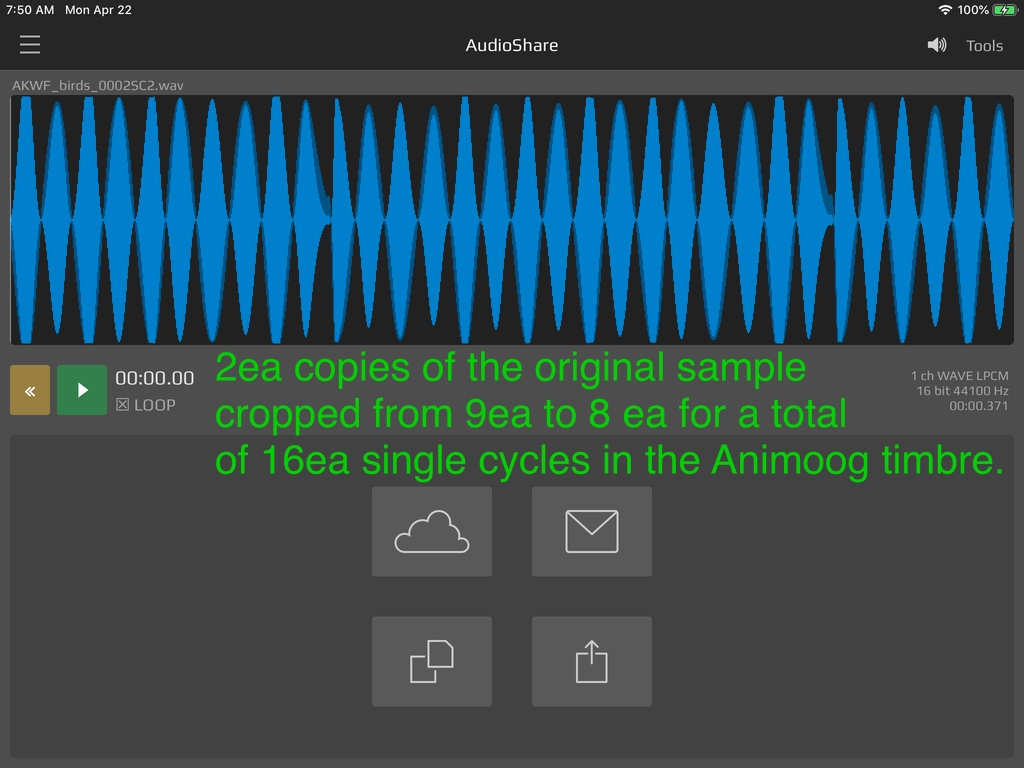
Perhaps the safest route would be to transpose down the Animoog timbre you’ve created via MIDI to capture the frequency of the original samples?
When creating an Animoog preset composed of 8 timbres and you use timbres with different tunings, you can’t use MIDI note transposition to adjust for those frequency differences.
With more complex waveforms there will be more frequencies at different amplitudes (volumes) which will further complicate determining the dominant or root note of the single cycle waveform.